LOS NIVELES DE VAN HIELE

Van Hiele y los niveles de aprendizaje

¡Buenas viajemáticos! Hoy venimos a hablaros de los niveles de Van Hiele y su utilidad en el estudio de la geometría. Se trata de una teoría de enseñanza y aprendizaje de la geometría, diseñado por el matrimonio holandés van Hiele en el año 1957.

Es una teoría de enseñanza y aprendizaje de la geometría, diseñado por el matrimonio holandés Van Hiele. 

El modelo abarca dos aspectos: uno descriptivo, mediante el cual se identifican las diferentes formas de razonamiento geométrico de los alumnos y se puede valorar el progreso de estos y otro instructivo, el cual marca unas pautas a seguir por los profesores para favorecer el avance de los estudiantes en su nivel de razonamiento geométrico. 

Los Van Hiele proponen 4 niveles de razonamiento, estos no van asociados a la edad, y cumplen las siguientes características:

• No se puede alcanzar un nivel sin haber pasado por el nivel anterior, o sea, el progreso de los alumnos a través de los niveles es secuencial e invariante.

• Lo que es implícito en un nivel de pensamiento, en el nivel siguiente se vuelve explícito.

• Cada nivel tiene su lenguaje utilizado (símbolos lingüísticos) y la importancia de los contenidos (conexión de estos símbolos dotándolos de significado).

• Dos estudiantes con distinto nivel no pueden entenderse. 

Nivel 1. RECONOCIMIENTO

Los alumnos perciben las figuras geométricas en su totalidad, de manera global, como unidades. Además, perciben las figuras como objetos individuales, es decir que no son capaces de generalizar las características que reconocen en una figura a otras de su misma clase. Los estudiantes se limitan a describir el aspecto físico de las figuras, no suelen reconocer las partes de las que se componen, ni sus propiedades matemáticas. Las descripciones de las figuras están basadas en sus semejanzas con otros objetos (no necesariamente geométricos) que conocen; suelen usar frases como “...se parece a...”, “...tiene forma de...”, etc. Los estudiantes no suelen reconocer explícitamente las partes de que se componen las figuras ni sus propiedades matemáticas.

Nivel 2. ANÁLISIS

Los estudiantes se dan cuenta de que las figuras geométricas están formadas por partes y que están dotadas de propiedades matemáticas; pueden describir las partes de una figura y enunciar sus propiedades. Además de reconocer las propiedades matemáticas mediante la observación de las figuras y sus elementos, los estudiantes pueden deducir otras propiedades generalizándolas a partir de la experimentación. Sin embargo, no son capaces de relacionar unas propiedades con otras, por lo que no pueden hacer clasificaciones lógicas de figuras basándose en sus elementos o propiedades.  

Nivel 3. CLASIFICACIÓN

En este nivel comienza la capacidad de razonamiento matemático de los estudiantes. Ya son capaces de reconocer que unas propiedades se deducen de otras y de descubrir esas implicaciones; en particular pueden clasificar lógicamente las diferentes familias de figuras a partir de sus propiedades o relaciones ya conocidas. No obstante, sus razonamientos lógicos se siguen apoyando en la manipulación. Los estudiantes pueden describir una figura de manera formal, es decir, pueden dar definiciones matemáticamente correctas, comprenden el papel de las definiciones y los requisitos de una definición correcta. Si bien los estudiantes comprenden los sucesivos pasos individuales de un razonamiento lógico formal, lo ven de forma aislada, no entienden la necesidad de encadenamiento de estos pasos, ni entienden la estructura de la demostración. Al no ser capaces de realizar razonamientos lógicos formales ni sentir su necesidad, los alumnos no comprenden la estructura de las matemáticas.

Nivel 4. DEDUCCIÓN FORMAL

Alcanzando este nivel, los estudiantes pueden entender y realizar razonamientos lógicos formales; las demostraciones (de varios pasos) ya tienen sentido para ellos y sienten su necesidad como medio para verificar la verdad de una afirmación. Comprenden la estructura axiomática de las matemáticas, es decir el sentido de la utilidad de términos no definidos, axiomas, teoremas,... Los estudiantes aceptan la posibilidad de llegar al mismo resultado desde distintas premisas, la existencia de definiciones equivalentes del mismo concepto..

Van Hiele caracteriza el aprendizaje como resultado de la acumulación de experiencias adecuadas; por lo tanto, existe la posibilidad de alcanzar niveles más altos de razonamiento fuera de la enseñanza escolar si se consiguen las experiencias apropiadas. No obstante, esas experiencias, aunque existen y no deben despreciarse, generalmente no son suficientes para producir un desarrollo de la capacidad de razonamiento completo y rápido, por lo que la misión de la educación matemática escolar es proporcionar experiencias adicionales, bien organizadas, para que sean los más útiles posibles. Para ello el matrimonio propone 5 fases, las cuales de dan en cada uno de los niveles (Información, orientación dirigida, explicitación, orientación libre, integración). A lo largo de estas fases, el docente debe procurar que sus alumno construyan la red mental de relaciones del nivel de razonamiento al que deben acceder, creando primero los vértices de la red, y después las conexiones entre ellos. Dicho de otra manera es necesario conseguir en primer lugar, que los estudiantes adquieran de manera comprensiva, los conocimientos básicos necesarios, (nuevos conceptos, propiedades,vocabulario...) con los que tendrán que trabajar, para después centrar su actividad, en aprender a utilizarlos y combinarlos. 

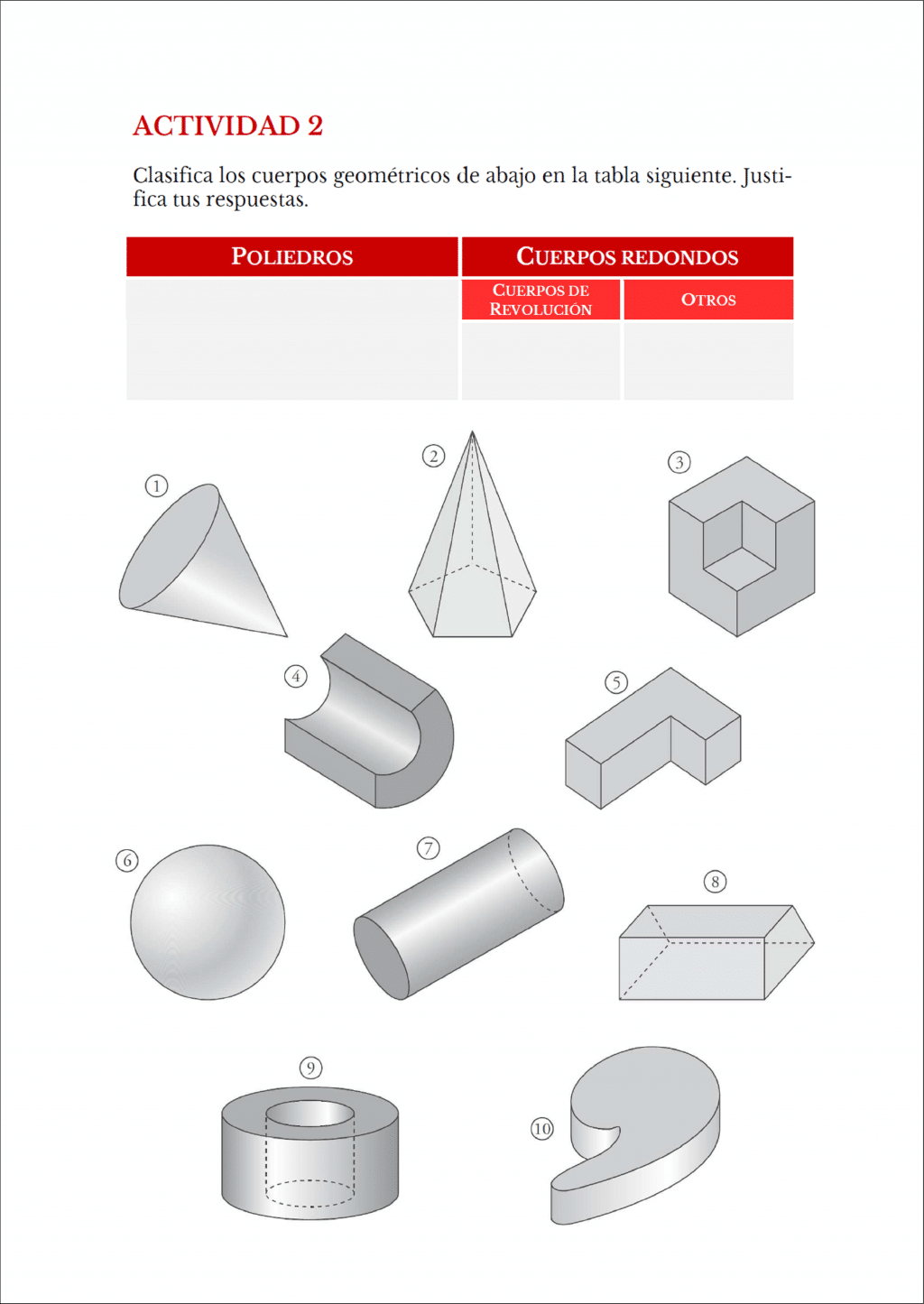
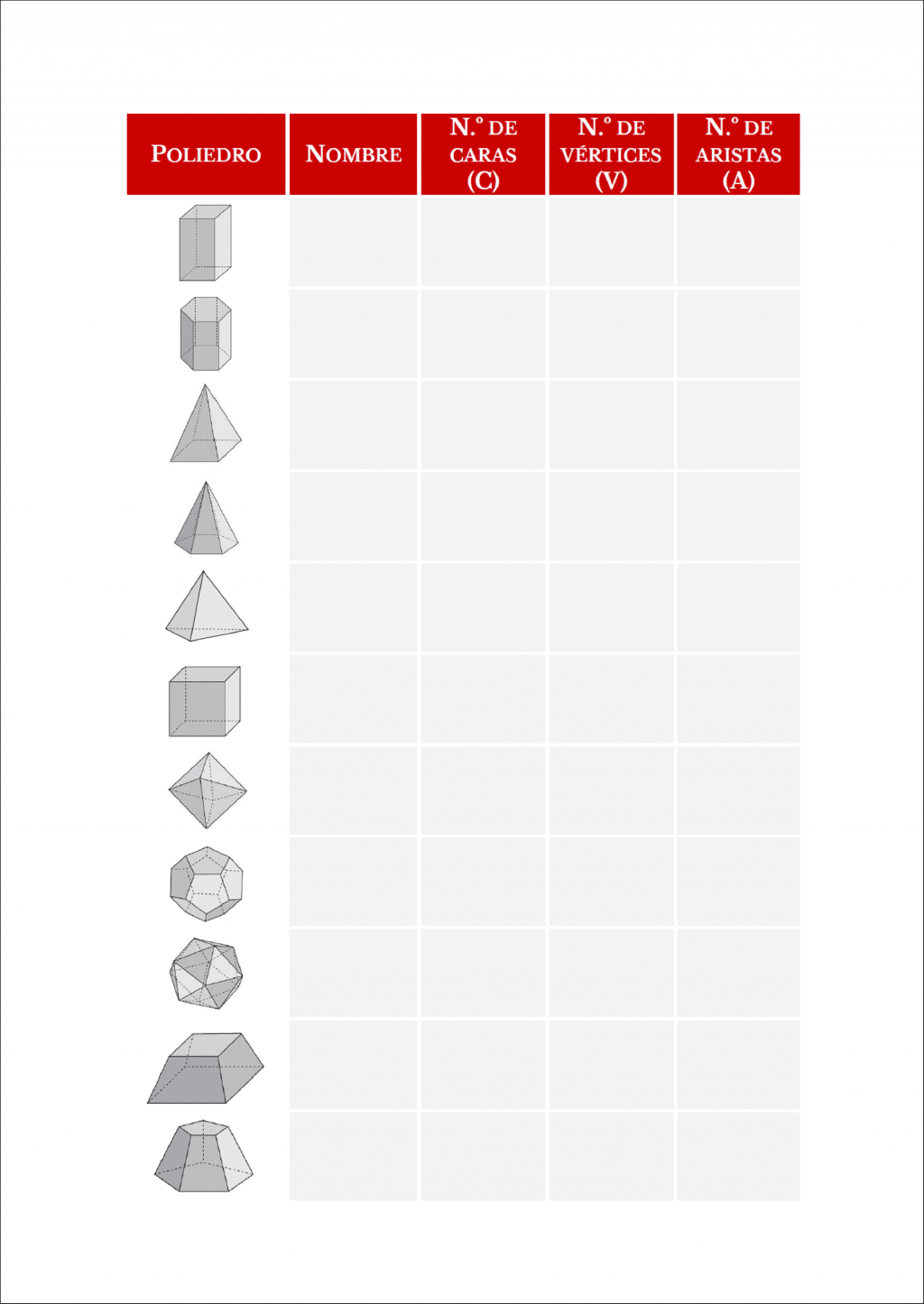
A continuación, dejamos algunas fichas con actividades que creemos que son interesantes para trabajar los distintos niveles de Van Hiele.

 

     Además, dejamos por aquí abajo unos vídeos muy interesantes con la explicación de los niveles de Van Hiele.¡DISFRUTARLOS!